It is with great pleasure that I post this article by Dr. rer. nat. Jochem Hauser, Scientific Director of HPCC-Space GmbH on the significance of the recent discovery of gravitational waves. Dr. Hauser is the co-originator of Extended Heim Theory along with Dr. Walter Dröscher.
Image: ©2015 S. Ossokine , A. Buonanno (MPI for Gravitational Physics)/W. Benger (Airborne Hydro Mapping GmbH)
On 11 February 2016 the LIGO and VIRGO Collaboration groups reported on the detection of gravitational waves as predicted by Einstein’s GR in 1916. The signals were actually measured in September 2015, but the teams took time to verify their results, most likely to avoid the embarrassment of the BICEP2 experiment.
However, the gravitational wave detection was hailed by numerous journals and newspapers as a revolution in physics, providing much incorrect information, not to say hype. For instance, read the partly unscientific language used in Scientific American about this effect.
It should be noted that there was already a Nobel prize for the indirect detection of gravity waves in 1993 (Hulse & Taylor) based on the orbital period of a binary star system. Hence, their direct measurement is not a surprise at all. The energy radiated (narrowing the joint orbit) from the binary pulsar PSR 1913+16 has been calculated from linear theory and exactly matches the observations.
In the first edition of this book it was already stated that Einstein’s GR is the only answer to gravitational fields in the cosmological realm and all competing theories are more or less ruled out. But this does not mean that extensions to GR are impossible or unnecessary.
According to EHT any gravitational theory predicting gravity must be fully compatible with Einstein’s GR, except for predictions of physical processes that take place inside a black hole. Even for very small accelerations it seems unlikely that GR will fail. It should be noted, however, that according to the late German physicist B. Heim, gravitational attraction disappears (is zero) at distances comparable to the Schwarzschild radius rS. Is this were the case, there would be no gravitation inside a black hole, and matter within the black hole would enjoy some kind of asymptotic freedom, similar to quarks in a proton or neutron.
It is important to note that gravitational plane waves (reducing the degrees of freedom in the metric tensor) are predicted by the linearized Einstein equations that are similar to the Maxwell equations. However, GR is a nonlinear theory. In order to confirm Einstein’s non-approximated GR, one must first ascertain that the nonlinear field equations of Einstein allow for waves also. They do. This is not trivial as there is, in principle, graviton-graviton interaction. The graviton particle as the mediator boson for gravity follows from the duality between the metric field hμν and the particle picture, that is, this concept of quantum mechanics is introduced into GR. Because photons do not carry electric charge themselves they are not subject to this kind of nonlinear interaction. The metric field is a second rank tensor and it can be shown that gravitons must have spin 2. The proof is difficult because this must hold in the relativistic case, too, see E. Wigner 1939, while the photon has spin 1.
The crucial point therefore is: can the gravitational signals detected be interpreted with Einstein’s linearized equations or are the full nonlinear equations needed? It seems, from the black hole masses involved (about 29 and 36 solar masses), that the linear theory may not match the measured data (this needs still to be confirmed). Relativistic (nonlinear) effects become spectacular, when GM/rc2 ≈ 1. The merger of these two black holes is assumed to have taken place at half the speed of light with a final orbital period of about 250 Hz. The two black holes are then supposed to have coalesced into a single black hole with the equivalent of about 62 solar masses. This scenario is the accepted physical interpretation for the time being – provided of course that no other, more plausible, alternatives can be found. If, however, these two black holes, supposed to have generated the gravitational waves, possess an extension similar to the diameter of the Sun, the magnitude of the relativistic gravitational effects becomes about 6 − 8 × 10−5 on the surface of the black hole, and the linear theory should be correct. On the other hand, astronomers have, for the first time, measured the radius of a black hole in September 2012 and are claiming that it is about 5.5 ×rS , where rS is the Schwarzschild radius (light cannot escape from the black hole if it is closer than rS). For the Sun rS ≈ 2.95 km. In general, it is believed that black holes have a Schwarzschild radius rS about 100,000 times smaller than the Sun. If this were the case, then the gravitational waves detected would be a confirmation of the validity of the nonlinear field equations, provided of course, that the underlying assumption of two merging black holes as the source for gravitational waves is correct.
If the effect can be explained by the linearized field equations, then any gravitational theory that gives the same linearized equations as Einstein’s theory would have passed the test, too.
There is, however, another principle to detect gravitational waves of low frequency – which cannot be measured by LIGO – based on the usage of compact gravity pulsars that are also emitting radio waves. The goal is to measure the changes in the distances between the Earth and the pulsars caused by the spacetime distortion created by the emitted gravitational waves, when they are passing over the Earth. This change in distance is causing a delay or advance in the radio pulse arrival time. Because this effect is extremely small, M. Kramer et al. at MPI Bonn, Germany are searching for the most rotationally stable pulsars, known as millisecond pulsars.
In conclusion, the experiments seem to have found gravitational waves, but this effect might be explained by a linearized gravitational theory. Moreover, if Einstein’s nonlinear equations turn out to be necessary to explain these results (more likely), we are talking about the science of November 1915.
The much more important question remains unanswered, as pursued by Einstein from 1915 till the end of his research activity: is there an interaction between gravity and electromagnetism? This means are there gravitational fields that are not cosmological fields, that is, whose source are not static or moving large masses? Hints for the existence of these gravitational fields may be found in the recent experiments by Tajmar, Graham and Gravity Probe B experiment as discussed in detail in Sec. 8 of “Introduction to Physics, Astrophysics and Cosmology of Gravity-Like Fields.”
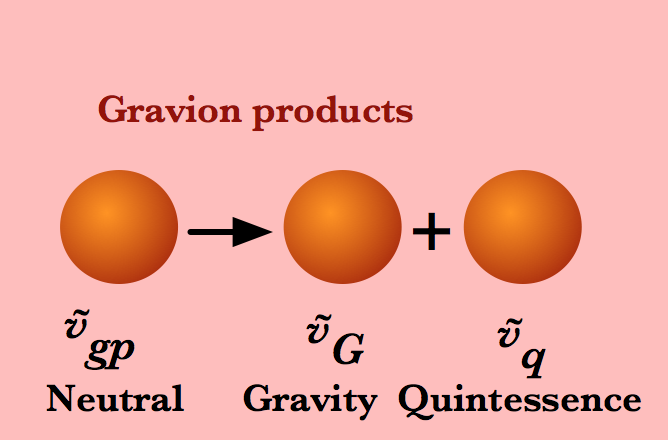
Theory, in the form of EHT, is predicting such a conversion from electromagnetism to gravitation, induced by the phenomenon of symmetry breaking (not known at Einstein’s time), and GR consequently needs to be supplemented by these so called conversion fields, i.e., those gravitational fields resulting from electromagnetic fields. This means that three additional gravitational particles (bosons) are proposed, allowing the generation of gravity-like fields similar to the generation of magnetic fields.
From an experimental point of view, however, the LIGO measurements are extremely sophisticated. The teams claim to be able to see distance changes in the range of 10−19 m that is much less than the radius of a proton!
A polarized gravitational wave traveling in one direction acting on a circle of particles is leading to an oscillatory motion, compressing and elongating the diameter of the circle, forming an elliptic shape, but also does rotate the axis of the ellipse. Hence, a signal in both arms of the laser interferometer should be detected.
As a next step, the space antenna LISA Pathfinder from ESA will begin operating in March 2016. We may expect to see a confirmation of gravitational waves by the full scale experiment eLISA, planned for 2028.
Jochem Hauser, 18 February 2016
edited 29 Feb 2016 – GD